编译原理(ε-NFA和NFA和DFA)

DFA与NFA

一个状态Q需要跳转,跳转条件包括每一个sigma的集合,但同时针对于NFA,我们引入了一个ε,对应的集合其实实际上是空集

∑*:所有字符的组合和ε,即从一个字符和多个字符的组合,一个单词的无限重复构成新的单词

ε-NFA与NFA

A为初始状态,D为终止状态

考试会考:给出一个NFA或者DFA状态图,转换成表,或者相反过来

思考: 一个NFA和ε-NFA之间的关系

• 任意的不带ε对于带的,可以视为任意的状态和空集作为参数调用状态转移函数依然还等同于他自身,这样可以视为不带有ε的子集

对于带ε对于不带的,二者之间应该如何去转换呢?

• 发现要想要合并,则两个接收相同状态的合并了,则会导致构成一个环,将会改变条件,出现二者重复接收同样的条件,将会永远循环.
• 通过添加边的方式,来实现去除原本的ε边,实现状态的转换

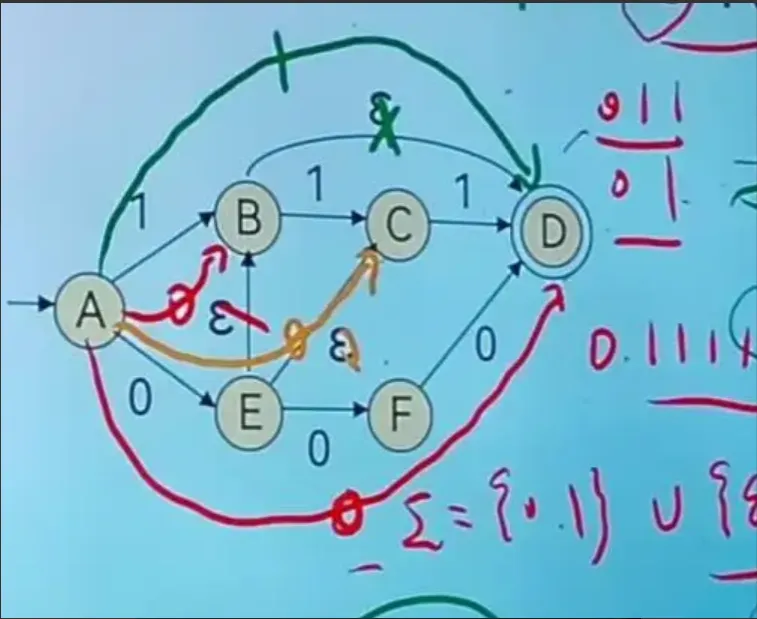
εεε=ε :连着几个ε其实是一样的

解决方法: 只要通过ε到达的状态,都去添加一条边直达ε最终指向的状态

1. 先判断到达ε边之前的边和状态
2. 将所有的ε边去除掉,同时添加一条边从到达ε边之前的状态,将原有的到达ε边之前的状态的条件作为新的边的条件,然后指向到无论几个ε到达的边

如何找边:

转换为:
给定一个状态,找以ε为边可达的状态,本质上变成对一个树的遍历.
可以寻找闭包:用深度优先遍历或者广度优先遍历均可

示例:

Unix系统:文件查找用的也是类似有限状态自动机的原理,所以很快.

---

RE正则表达式:

刻画了一个描述语言的规则: 语言:字符串构成的集合
自然语言有大量的环境,语法等规则,形式语言则可以有特定的规则,可以由DFA,NFA等有限状态机去刻画.

程序语言->形式语言

证明RE和ε-NFA等价则NFA等价则DFA等价

表达式到字符串的一个定义,下述均为正则表达式(三个基础表达式)

• L{a}={a}:字符串为1的,类型是字符
• L{ε}={ε}:字符串为空,类型是空字符串
• L{∅}={∅}:空集,类型是集合

正则表达式运算定义:

1. E1+/-E2相加减的也是一个E;
2. E1+∅结合的也是一个E;
3. E1*E2或者E1/E2结合的也是一个E;

字符串的构建规则:

1. L(E1+E2)=L(E1)∪L(E2)—>{E1,E2}集合
2. L(E1·E2)=L(E1·L(E2)—->{w|w=w1w2 ,w1,w2}原来两个语言的拼接
3. L(E1*)———>L(A)*–>{ε,a,aa,aaa,aaaa,aaaaa,…..}

---

L(A*ε)=? ,依然还是集合A的元素与ε进行拼接导致结果还是一个{A}

L(A*∅)=?,结果是空集,原因与上面相同

L(A*)=?依然是字符串的拼接—>其中的含义是闭包,L(A)=L(A)*–>{ε,a,aa,aaa,aaaa,aaaaa,…..}

表达式的优先级:

*>@>∪:闭包>拼接>取并集

会考:

最后一个的答案: 最后一个组成的字符串当中0一定会是三的倍数

概念:其实指的会是一个循环的概念,会出现多次,但是多少次无法去最终确定